Case Study: Shortfalls of Attention is All You Need

This is drawn from Section 1.3 of my paper Neural Circuit Diagrams: Robust Diagrams for the Communication, Implementation, and Analysis of Deep Learning Architectures. It is a primer for a series of posts I am about to make on how Neural Circuit Diagrams can address many pressing problems in the deep learning field.

To highlight the problem of insufficient communication of deep learning architectures, I present a case study of Attention is All You Need, the paper that introduced transformer models. Introduced in 2017, transformer models have revolutionized machine learning, finding applications in natural language processing, image processing, and generative tasks.

Transformers' effectiveness stems partly from their ability to inject external data of arbitrary width into base data. I refer to axes representing the number of items in data as a width, and axes indicating information per item as a depth.

An attention head gives a weighted sum of the injected data's value vectors, $V$. The weights depend on the attention score the base data's query vectors, $Q$, assign to each key vector, $K$, of the injected data. Value and key vectors come in pairs. Fully connected layers, consisting of learned matrix multiplication, generate ${\displaystyle Q}$, ${\displaystyle K}$, and ${\displaystyle V}$ vectors from the original base and injected data. Multi-head attention uses multiple attention heads in parallel, enabling efficient parallel operations and the simultaneous learning of distinct attributes.

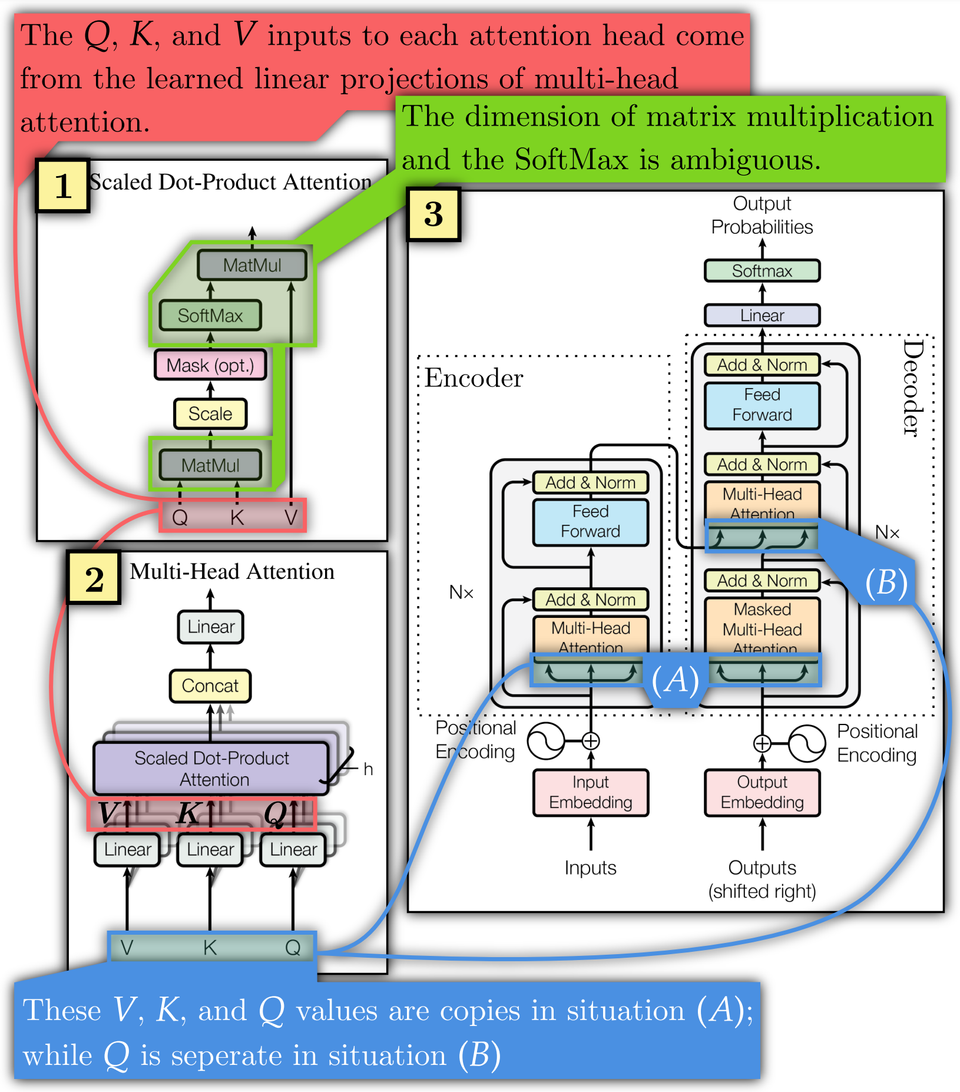
Attention is All You Need, which I refer to as the original transformer paper, explains these algorithms using diagrams and equations, given below, that hinder understandability (this is also addressed in other papers).

$\text{(1) Attention}( Q,K,V) =\text{SoftMax}\left(\frac{QK^{T}}{\sqrt{d_{k}}}\right) V\ \text{(} d_{k}\text{ is the key depth})$

$\text{(2) MultiHead}( Q,K,V) =\text{Concat}(\text{head}_{1}\text{, ...,}\text{head}_{h}) W^{O}$

$\text{(3) where }\text{head}_{i} =\text{Attention}\left( QW_{i}^{Q} ,KW_{i}^{K} ,VW_{i}^{V}\right)$

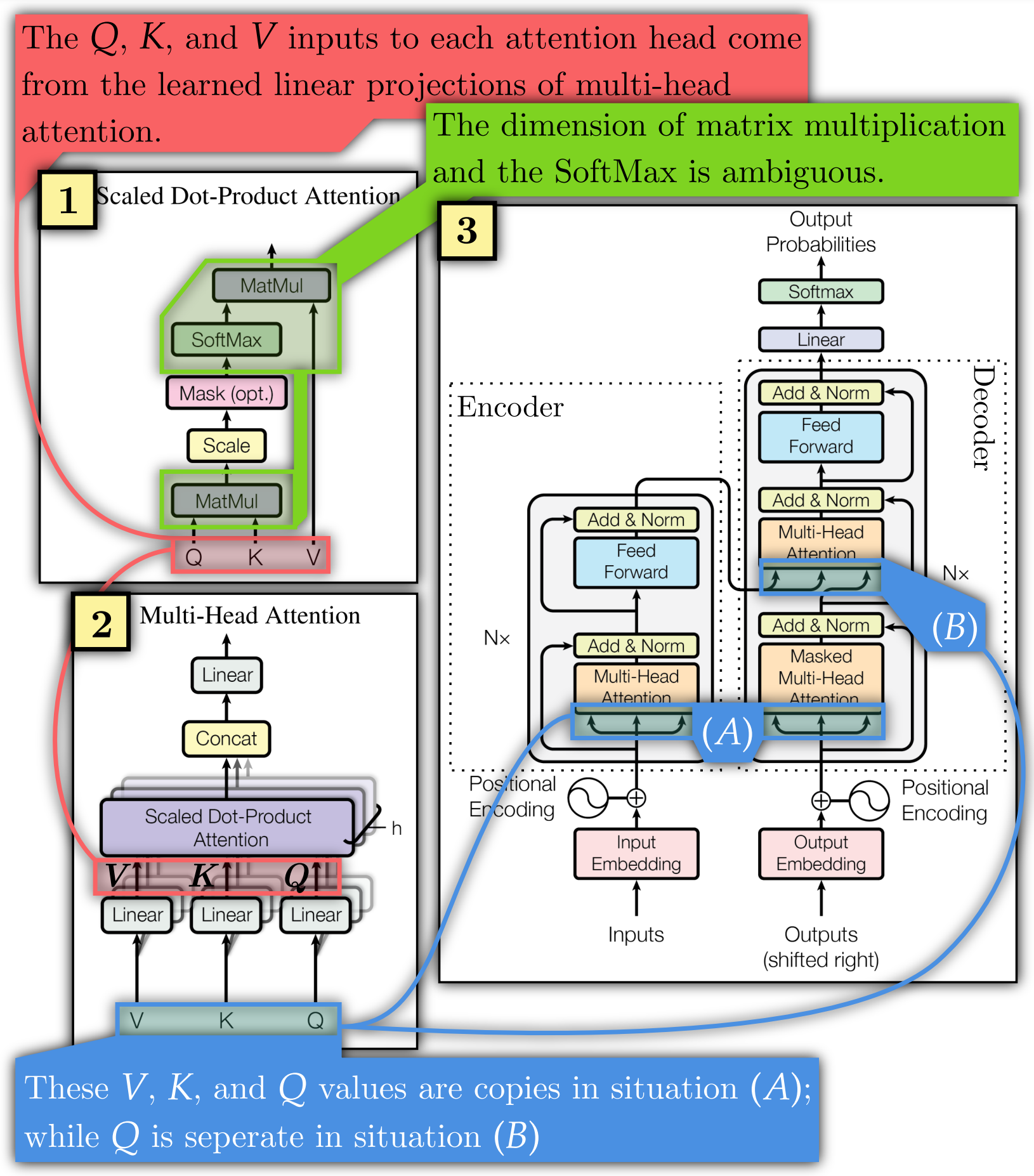
The original transformer paper obscures dimension sizes and their interactions. The dimensions over which SoftMax and matrix multiplication operate are ambiguous (Figure 1.1, green; Equation 1, 2, 3).

Determining the initial and final matrix dimensions is left to the reader. This obscures key facts required to understand transformers. For instance, $K$ and $V$ can have a different width to $Q$, allowing them to inject external information of arbitrary width. This fact is not made clear in the original diagrams or equations. Yet, it is necessary to understand why transformers are so effective at tasks with variable input widths, such as language processing.

The original transformer paper also has uncertainty regarding $\displaystyle Q$, $\displaystyle K$, and $\displaystyle V$. In Figure 1.1 and Equation 1, they represent separate values fed to each attention head. In Figure 1.2 and Equation 2 and 3, they are all copies of each other at location (A) of the overall model in Figure 1.3, while $\displaystyle Q$ is separate in situation (B).

Annotating makeshift diagrams does not resolve the issue of low interpretability. As they are constructed for a specific purpose by their author, they carry the author's curse of knowledge. In Figure 1, low interpretability arises from missing critical information, not from insufficiently annotating the information present. The information about which axes are matrix multiplied or are operated on with the SoftMax is simply not present.

Therefore, we need to develop a framework for diagramming architectures that ensures key information, such as the axes over which operations occur, is automatically shown. Taking full advantage of annotating the critical information already present in neural circuit diagrams, I present alternative diagrams in Figures 20, 21, and 22 (which you can find in the paper!).